Identifying the characteristic cloud size distributions that make up a cloud
Submitter
Shaw, Raymond A
— Michigan Technological University
Area of Research
Cloud Processes
Journal Reference
Allwayin N, M Larsen, A Shaw, and R Shaw. 2022. "Automated identification of characteristic droplet size distributions in stratocumulus clouds utilizing a data clustering algorithm." Artificial Intelligence for the Earth Systems, 10.1175/AIES-D-22-0003.1. ONLINE.
Science
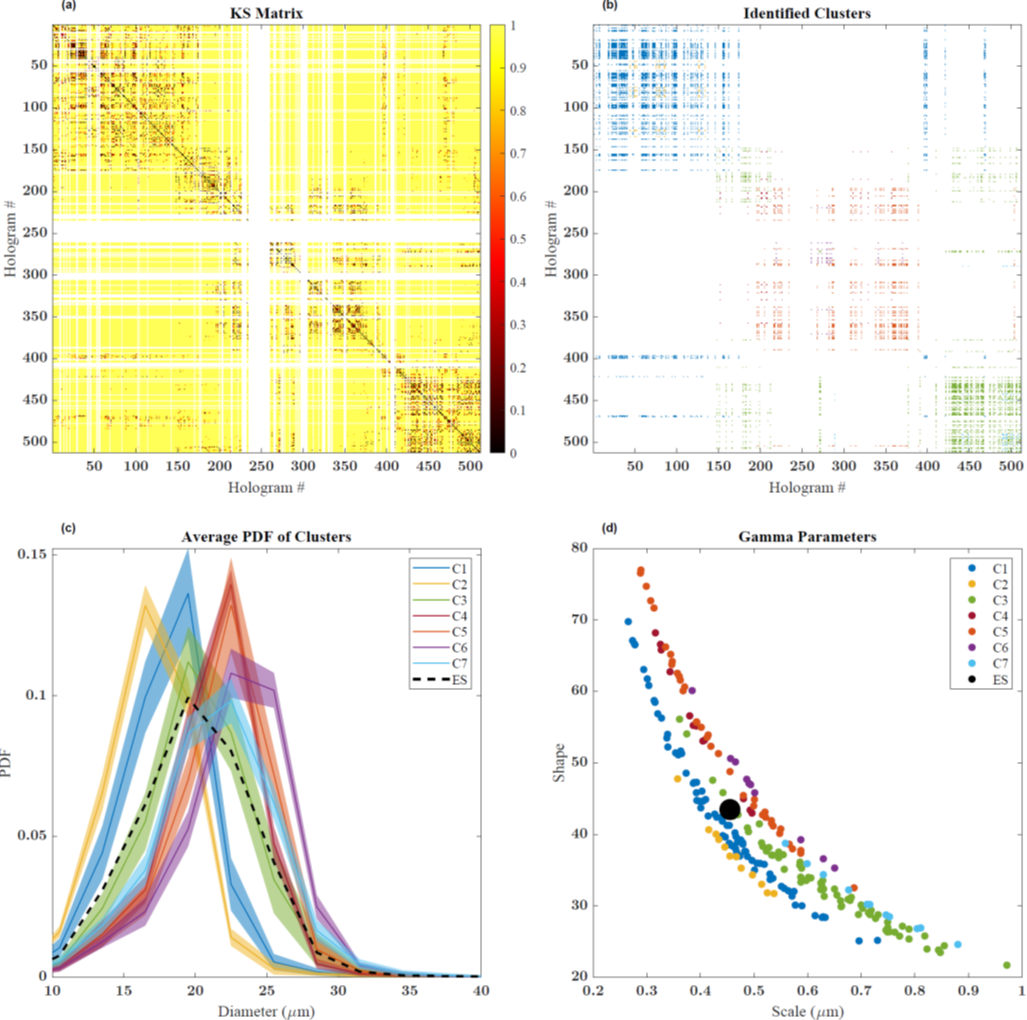
Figure 1. (a) A matrix resulting from comparing each hologram with every other hologram recorded during a level flight through a stratocumulus cloud. (b) Colored according to the similar holograms identified by a data clustering algorithm. (c) Distributions of the identified “characteristic” clusters. The dashed black line shows the cloud average. (d) The fitted shape and scale parameters of the modified gamma distribution for the holograms in different clusters. The black dot is for the entire segment. From journal.
Cloud droplet size distributions are often represented in global climate models (GCMs) and remote-sensing algorithms in idealized forms (modified gamma distributions) that capture the average behavior across a large spatial domain. Cloud processes, such as growth by condensation or collisions, conversely “see” a range of spatial scales and are often influenced by processes at the droplet scale. We ask the question whether a population of droplets at any point in a homogenous-looking cloud resembles the average distribution measured from the entire cloud. In other words, do the cloud droplet size distributions sampled at different points in a cloud look like they come from the global distribution? Further, we investigated whether there is any similarity between the droplet populations at different points in a cloud. We performed hypothesis testing to evaluate this possibility and developed an algorithm that identifies a distinct set of cloud size distributions that completely represent all the subsamples in a cloud.
Impact
A major challenge in climate models and remote-sensing algorithms in representing clouds is capturing interactions at droplet scales: parameterizations are used for idealized, grid-averaged droplet size distributions and do not account for the variability key to nonlinear processes relevant to precipitation growth. Our algorithm identifies a set of characteristic cloud size distributions that together have the potential to characterize the sub-grid-scale variability and improve cloud representations in climate models.
Summary
Using standard hypothesis-testing and data-clustering algorithms on in situ field measurements from the Aerosol and Cloud Experiments in the Eastern North Atlantic (ACE-ENA) campaign, we evaluated the possibility of obtaining a characteristic set of cloud droplet size distributions for a homogenous stratocumulus cloud sample. Droplet populations at the centimeter scale were obtained from measurements made by the Holographic Detector for Clouds (HOLODEC) cloud probe. The Kolmogorov–Smirnov (KS) test compares two of these populations to determine if they are from the same parent distribution. For a series of N locations in the cloud, all cross-comparisons yield N^2 results that can be arranged as a matrix of KS results. Similar cloud size distributions are then grouped from this matrix, drawing from data-clustering methods used in machine learning like Density-Based Spatial Clustering of Applications with Noise (DBSCAN). The cluster members thus identified by the algorithm have similar cloud size distribution shapes. These clusters together form a characteristic set of droplet size distributions that combine to form the cloud-averaged distribution. Individual cluster members are also fitted to modified gamma distributions and the range of parameters (shape and scale) obtained from a wide range around those values used in GCMs.
Keep up with the Atmospheric Observer
Updates on ARM news, events, and opportunities delivered to your inbox
ARM User Profile
ARM welcomes users from all institutions and nations. A free ARM user account is needed to access ARM data.


















